If one row has a child and that child has a child and so on…
How many descendants does the original item have in total?
Here is a doc with desired results and a visual that explains what I’d like to achive:
I’m on it @Fran_Vidicek 
1 Like
Well, let’s go @Fran_Vidicek, lock your belt . It’s a bit tricky, and may be @Paul_Danyliuk will find a non-dynamical way to solve that. But it works !!!
We will use a while loop, each step will iteratively calculate the child(s) of items, as long as there is at least one child. We will calculate the sum of the child and increase the total number each time. Once the child column is blank, the while loop will stop.
Here is what it looks like
I need :
- a Start button = Init + Run
- An init button = that will set the first Child
- A Run button : that will change the child list to next generation, and update the total number
- A loop : that will trigger again Run button as long as there are children
- A condition (checkbox) column : that will check if there are still children
To process that :
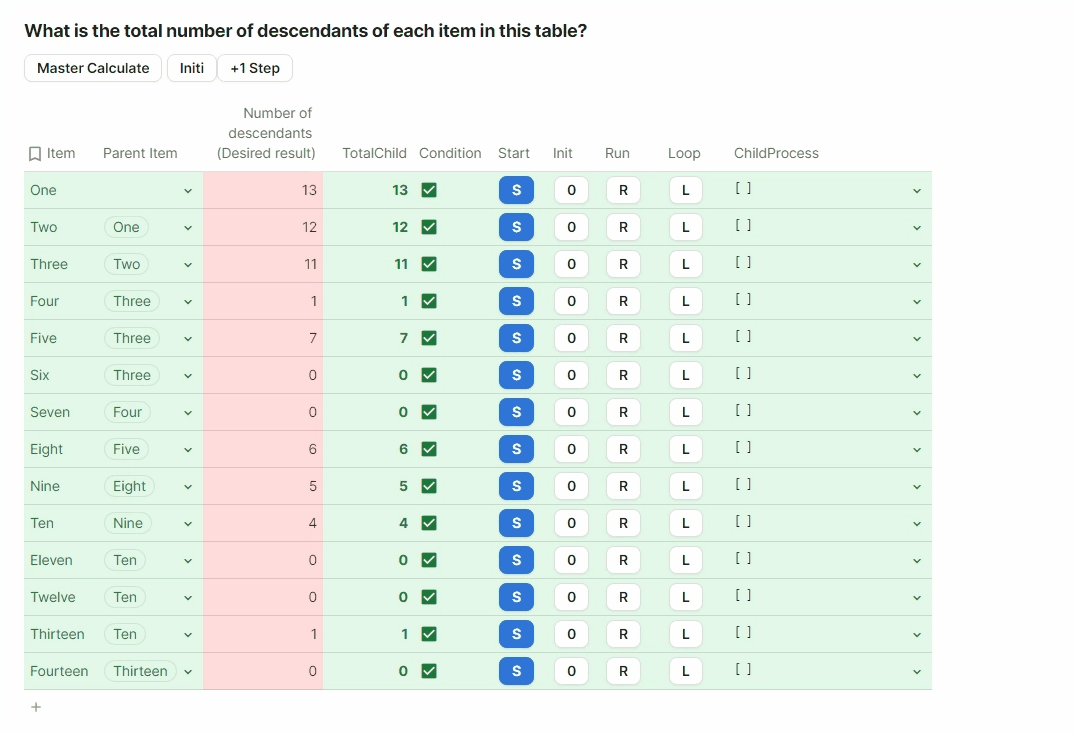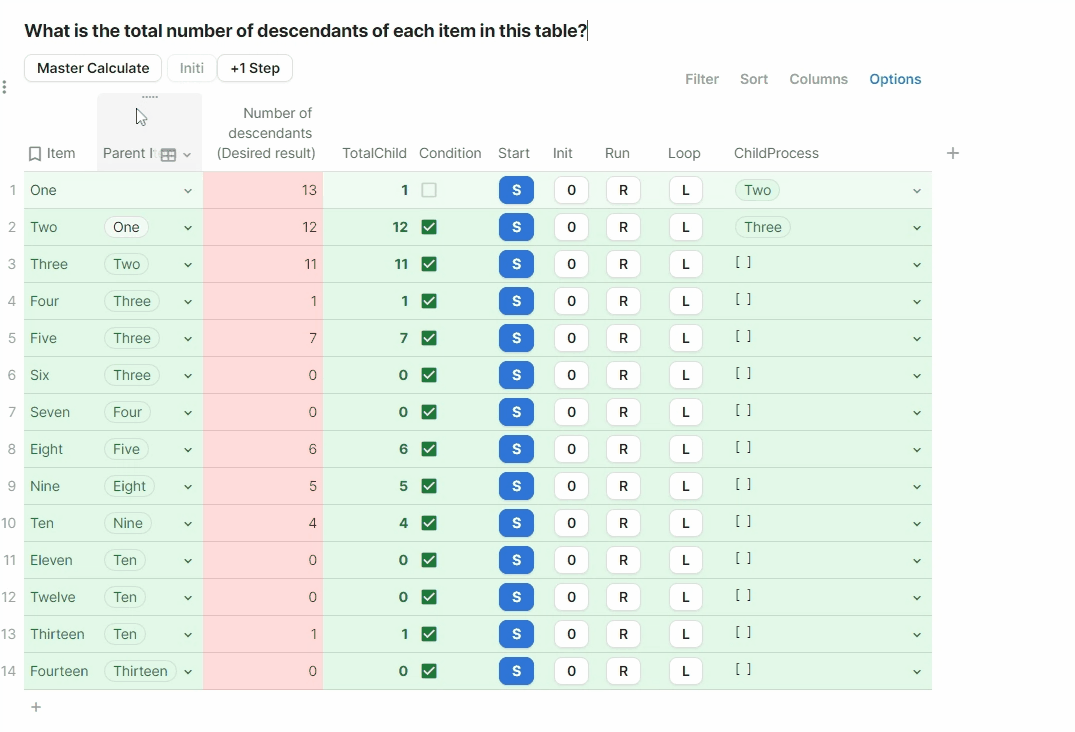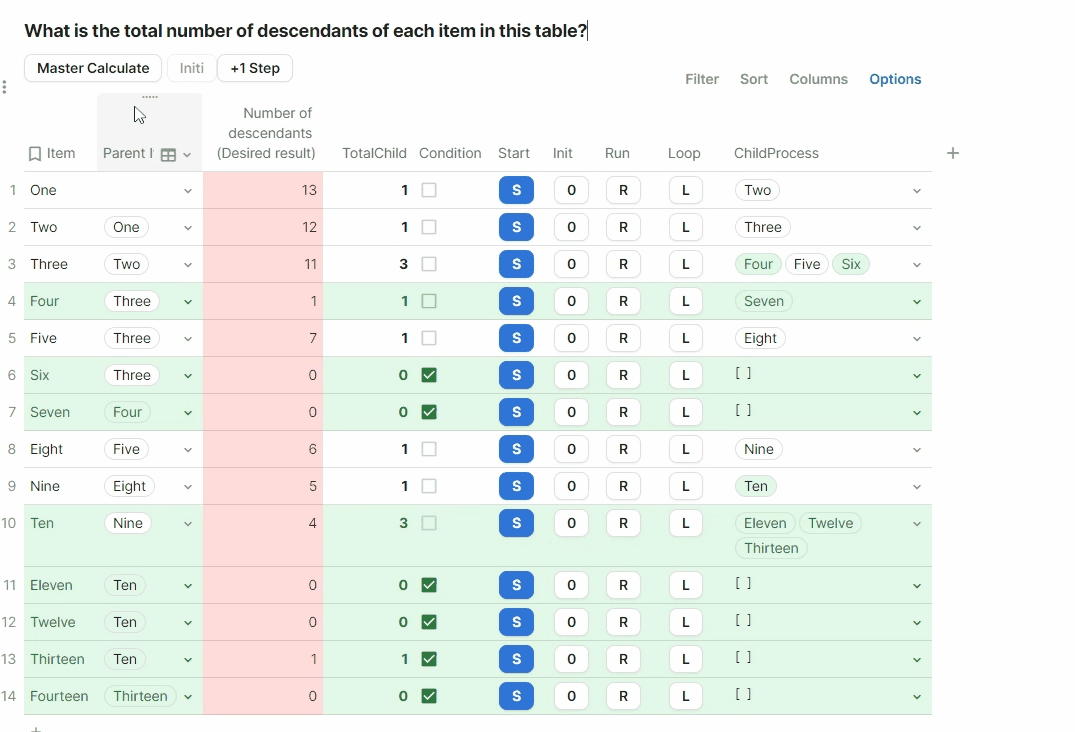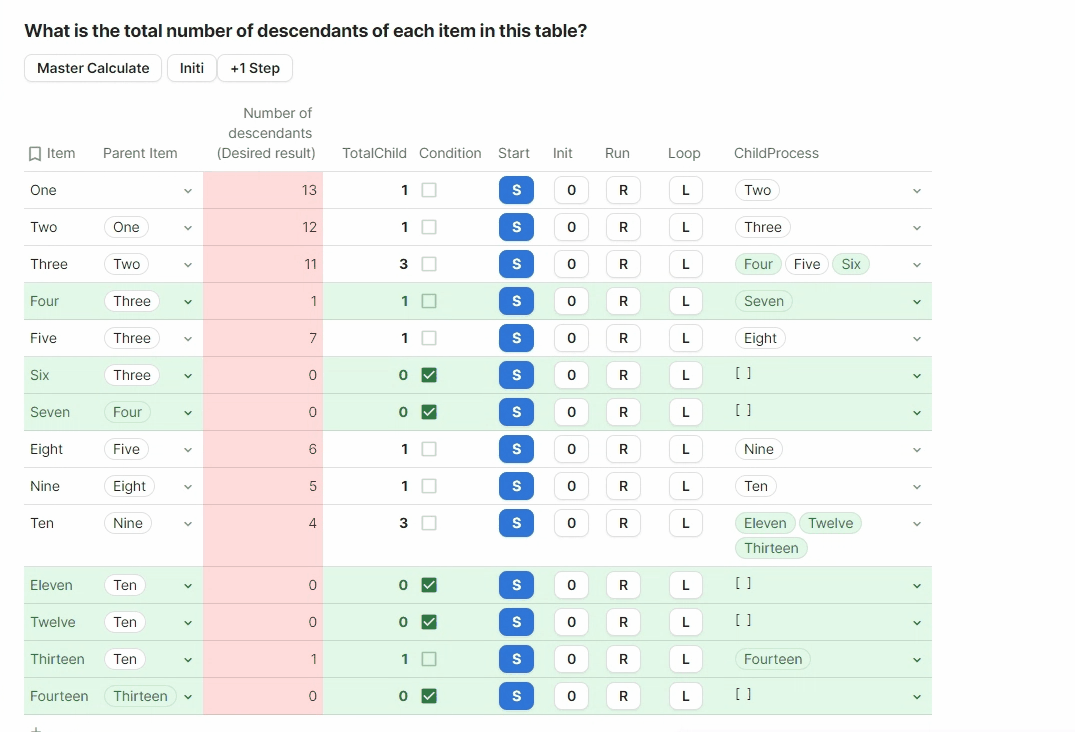
Start by setting an initalization column. This will find, for each row, what is the first level of child. We need that before we start our loop, and we store thoses values inside ChildProcess column. But as we want to initialize only once, we need to put it outside of the loop. You can see that we initialize also the number of child.
If I show you this step only, this is the result i got with only “initialization” process.
OK, then the core of the process is in the Run button, the code is here but please check it directly in embed doc for better view
RunActions(
WithName(
thisTable
.Filter(
[Parent Item].Contains(thisRow.ChildProcess)
),
Child,
RunActions(
ModifyRows(
thisRow,
thisRow.TotalChild,
thisRow.TotalChild +
if(thisRow.ChildProcess.IsBlank(), 0, Child.Count()),
thisRow.ChildProcess,
Child
)
)
),
thisRow.Loop
)
In a few word, this action will :
- Define what a child is : a child is an item from this table that contains current childprocess row. Step by step, we will check child, great child, etc…
- Modify the current row : we replace child process list with new child, and we add the total number of child from the begining to now.
- We call a Loop action → See next point
Now, we want to check if we still have child. If not we stop, if yes we continue. Then, I created a column Condition which only check if the child column is empty
Now, the loop button will call Run action again only if the condition is to false
This is really the core of the process :
- Initialize
- Update child list and add count to the total
- if there are still childs, continue, otherwhise stop it
Define a Start Button, that will initialize and start the first run
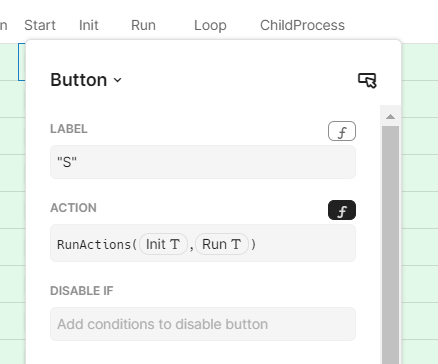
Finally Add a master button that will activate each start button !
And now the magic happens !
I truly realize this require a good level regardinf formula, but do not hesitate if I need to add some explanations
Find embed doc bellow
1 Like
Thanks once again 
, this should work well for my use case!
I think there may be a simpler way here.
If you create a column called “# of Descendants”, set it to select rows with Parent.contains(thisRow) and then sum their # of descendants +1 each, you’ll get an automatic recursion down to the bottom.
Num Of Descendants Column Formula:
ThisTable.Filter([Parent Item].Contains(thisRow)).[Num of Descendants].Sum() + ThisTable.Filter([Parent Item].Contains(thisRow)).[Num of Descendants].Count()
1 Like
I have to bow, congrats for this efficiency @Billy_Jackson !
I got stuck in my reasoning when I said myself “I have to count until there is no child any more”, and that led me to the while loop. Sometimes brain not enough open-minded !
@Fran_Vidicek, I set Billy’s MUCH BETTER solution in the embed doc also
Of course, given the simplicty of it, do use it !!
Cheers
2 Likes
I already tried something like this, had the same idea but it only went 2 levels deep and now I got the same result, but I might have done something wrong.
Give me a minute, I will try again.
Oh, ok I see now, thanks so much @Billy_Jackson !!! That’s perfect!
I don’t think the formula works, I believe you accidentally referenced to a wrong column.
Because if I delete the Number of Descendants (Desired Result) column, Billy’s Solution is an error.
And if I reference it to the right Number of Descendants column, it gives an error as well. Sum() function needs to be a number or something.
Or am I missing something?
I think there is an extra column at play here. The key to this working is that the formula is summing ITS OWN COLUMN. So in this case, it should be summing “Billy’s Solution” rather than a separate filtered column
1 Like
Yes that’s it! 
Thanks once again.
Hey — just seeing this. The screenshot in your OP is coming from my “tree chart”, right?
There’s a hidden column to look up children; it’s rather straightforward:
To calculate the number of children recursively, all you need to do is make another column, Cumulative to calculate cumulative children:
ListCombine(
thisRow.[_Children (visible)],
thisRow.[_Children (visible)].Cumulative
)
and then .Count() them:
and that’s it 
3 Likes
Yes it’s from the “three chart” doc. I went there for solution or ideas at first because it deals with similar structure 
. I didn’t find the solution but it proved itself useful for visualizing the issue 
.
However now I have another problem/question if anyone is interested in helping solve. It's similar to precious problem but goes a level further:
Imagine we have boxes. Each box can have boxes and toys inside of it. The toys can be inside other boxes or in the box itself.
How would we count total number of toys inside a box?
I have explained the issue in detail in the same doc I shared in OP on a different page called “Problem 2”.
I’m assuming this time It won’t be possible to create a “non-dynamic” solution and we will have to approach it in a way that is more similar to @Quentin_Morel 's solution here. 
I think you can actually still take a similar approach.
We’re looking for Total Number of Toys inside box = Toys Directly in Box + Sum of toys directly in boxes of all descendants.
As we’ve seen, it’s pretty straightforward to calculate either the list of descendants (as per Paul’s solution) or the sum of items within them.
Here, you’re looking to create a column Total Toys Within =
Toys.filter([Parent Box].contains(thisRow)).Count() // Total Toys directly in box
+ Boxes.filter([Parent Box].contains(thisRow)).[Total Toys Within].Sum() // Sum of all toys in descendant boxes
1 Like
That only seems to go 2 levels deep.
If I didn’t do something wrong It only counts :
Total toys directly in box + Number of toys in immediate descendant boxes
The formula doesn’t have that “cascading” 
effect.
I have put the attempt in the doc if you don’t mind checking If I missed something
Yes, another column has snuck in there again and spoiled our recursivity.
Try this here:
1 Like
The key principle here for both of these examples has been to create recursion without writing for/while loops by writing a formula that references other iterations of itself.
So RowA.RecursionFormulaColumn = functionOf(rowN.RecursionFormulaColumn)
This rowN is - itself - a function of other iterations of that column, so on and so on, as determined by the parent/child structure.
I don’t know how Coda’s formulas are implemented, but my best guess is that they are almost certainly performing a version of Quentin’s solution, but on the back end of things.
1 Like
I don’t think I understand.
Even if I put this formula in only one column it doesn’t give desired result. I don’t know if that’s what you thought when you said:
Have you tried putting that formula within the column named [Total Toys Within]?
I’m seeing it working on my end if I do that.
1 Like
Yep that works 
Thank you soo much 
!
1 Like